Seventh Mississippi State - UAB Conference on Differential Equations and
Computational Simulations.
Electron. J. Diff. Eqns., Conference 17 (2009), pp. 81-94.
A third-order m-point boundary-value problem of Dirichlet type
involving a p-Laplacian type operator
Chaitan P. Gupta
Abstract:
Let
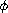 , be an odd increasing homeomorphisms from
, be an odd increasing homeomorphisms from
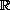 onto
onto
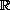 satisfying
satisfying
 , and let
, and let
![$f:[0,1]\times \mathbb{R}\times \mathbb{R}\times \mathbb{R}\mapsto \mathbb{R}$](gifs/ad.gif) be a
function satisfying Caratheodory's conditions.
Let
be a
function satisfying Caratheodory's conditions.
Let
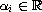 ,
,
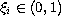 ,
,
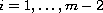 ,
,
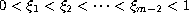 be given. We are interested in the
existence of solutions for the
be given. We are interested in the
existence of solutions for the
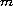 -point
boundary-value problem:
-point
boundary-value problem:
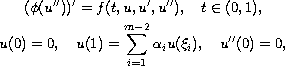
in the resonance and non-resonance cases. We say that this problem is at
\emph{resonance} if the associated problem
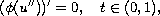
with the above boundary conditions has a non-trivial solution.
This is the case if and only if
 .
Our results use topological degree
methods. In the non-resonance case; i.e., when
.
Our results use topological degree
methods. In the non-resonance case; i.e., when
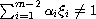 we note that the sign of
degree for the relevant operator depends on the sign of
we note that the sign of
degree for the relevant operator depends on the sign of
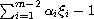 .
.
Published April 15, 2009.
Math Subject Classifications: 34B10, 34B15, 34L30.
Key Words: m-point boundary value problems; p-Laplace type operator;
non-resonance; resonance; topological degree.
Show me the PDF file (270 KB),
TEX file for this article.
 |
Chaitan P. Gupta
Department of Mathematics, 084
University of Nevada
Reno, NV 89557, USA
email: gupta@unr.edu |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
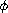 , be an odd increasing homeomorphisms from
, be an odd increasing homeomorphisms from
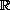 onto
onto
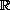 satisfying
satisfying
 , and let
, and let
![$f:[0,1]\times \mathbb{R}\times \mathbb{R}\times \mathbb{R}\mapsto \mathbb{R}$](gifs/ad.gif) be a
function satisfying Caratheodory's conditions.
Let
be a
function satisfying Caratheodory's conditions.
Let
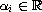 ,
,
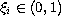 ,
,
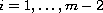 ,
,
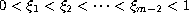 be given. We are interested in the
existence of solutions for the
be given. We are interested in the
existence of solutions for the
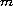 -point
boundary-value problem:
-point
boundary-value problem:
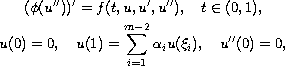
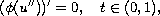
 .
Our results use topological degree
methods. In the non-resonance case; i.e., when
.
Our results use topological degree
methods. In the non-resonance case; i.e., when
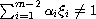 we note that the sign of
degree for the relevant operator depends on the sign of
we note that the sign of
degree for the relevant operator depends on the sign of
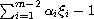 .
.
