We look for weak solutions
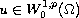 of the degenerate quasilinear Dirichlet boundary value problem
of the degenerate quasilinear Dirichlet boundary value problem
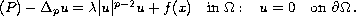
It is assumed that
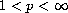 ,
,
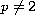 ,
,
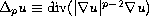 is the p-Laplacian,
is the p-Laplacian,
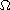 is a bounded domain in
is a bounded domain in
 ,
,
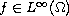 is a given function, and
is a given function, and
 stands for the (real) spectral parameter.
Such weak solutions are precisely the critical points of
the corresponding energy functional on
stands for the (real) spectral parameter.
Such weak solutions are precisely the critical points of
the corresponding energy functional on
 ,
,

I.e., problem (P) is equivalent with
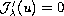 in
in
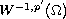 .
Here,
.
Here,
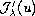 stands for the (first)
Frechet derivative
of the functional
stands for the (first)
Frechet derivative
of the functional
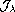 on
on
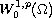 and
and
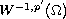 denotes the (strong) dual space of the Sobolev space
denotes the (strong) dual space of the Sobolev space
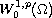 ,
,
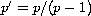 .
.
We will describe a global minimization method for this functional provided
 , together with the (strict) convexity
of the functional for
, together with the (strict) convexity
of the functional for
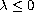 and possible "nonconvexity"
if
and possible "nonconvexity"
if
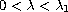 .
As usual,
.
As usual,
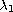 denotes
the first (smallest) eigenvalue of the positive p-Laplacian
denotes
the first (smallest) eigenvalue of the positive p-Laplacian
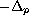 .
Strict convexity will force the uniqueness of a critical point
(which is then the global minimizer for
.
Strict convexity will force the uniqueness of a critical point
(which is then the global minimizer for
 ),
whereas "nonconvexity" will be shown by constructing a saddle point
which is different from any local or global minimizer.
These methods are well-known and can be found in many textbooks
on Nonlinear Functional Analysis or Variational Calculus.
),
whereas "nonconvexity" will be shown by constructing a saddle point
which is different from any local or global minimizer.
These methods are well-known and can be found in many textbooks
on Nonlinear Functional Analysis or Variational Calculus.
The problem becomes quite difficult if
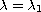 or
or
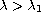 , even in space dimension one (N=1).
We will restrict ourselves to the case
, even in space dimension one (N=1).
We will restrict ourselves to the case
 ,
the Fredholm alternative for the p-Laplacian
at the first eigenvalue.
Even if the functional
,
the Fredholm alternative for the p-Laplacian
at the first eigenvalue.
Even if the functional
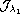 is no longer coercive on
is no longer coercive on
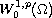 ,
for
,
for
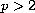 we will show that it is bounded from below and
does possess a global minimizer.
For
we will show that it is bounded from below and
does possess a global minimizer.
For
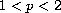 the functional
the functional
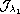 is unbounded from below and one can find a pair of
sub- and super-solutions to problem (P)
by a variational method (a simplified minimax principle)
performed in the orthogonal decomposition
is unbounded from below and one can find a pair of
sub- and super-solutions to problem (P)
by a variational method (a simplified minimax principle)
performed in the orthogonal decomposition
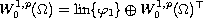
induced by the inner product in
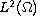 .
First, the minimum is taken in
.
First, the minimum is taken in
 ,
and then (possibly only local) maximum in
,
and then (possibly only local) maximum in
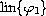 .
The "sub-" and "super-critical" points thus obtained provide
a pair of sub- and super-solutions to problem (P).
Then a topological (Leray-Schauder) degree has to be employed
to obtain a solution to problem (P)
by a standard fixed point argument.
.
The "sub-" and "super-critical" points thus obtained provide
a pair of sub- and super-solutions to problem (P).
Then a topological (Leray-Schauder) degree has to be employed
to obtain a solution to problem (P)
by a standard fixed point argument.
Finally, we will discuss the existence and multiplicity of a solution for problem (P) when
 "nearly" satisfies the orthogonality condition
"nearly" satisfies the orthogonality condition
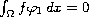 and
and
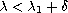 (with
(with
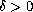 small enough).
A crucial ingredient in our proofs are
rather precise asymptotic estimates
for possible "large" solutions to problem (P)
obtained from the linearization of problem (P) about
the eigenfunction
small enough).
A crucial ingredient in our proofs are
rather precise asymptotic estimates
for possible "large" solutions to problem (P)
obtained from the linearization of problem (P) about
the eigenfunction
 .
These will be briefly discussed.
Naturally, the (linear selfadjoint) Fredholm alternative for
the linearization of problem (P) about
.
These will be briefly discussed.
Naturally, the (linear selfadjoint) Fredholm alternative for
the linearization of problem (P) about
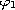 (with
(with
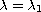 )
appears in the proofs.
)
appears in the proofs.
