Eighth Mississippi State - UAB Conference on Differential Equations
and Computational Simulations.
Electron. J. Diff. Eqns., Conference 19 (2010), pp. 37-44.
Quasireversibility for inhomogeneous ill-posed problems
in Hilbert spaces
Beth M. Campbell Hetrick
Abstract:
In a Hilbert space
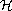 ,
the inhomogeneous ill-posed
abstract Cauchy problem is given by
,
the inhomogeneous ill-posed
abstract Cauchy problem is given by
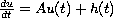 ,
,
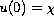 ,
,
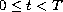 ;
where
;
where
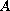 is a positive self-adjoint linear
operator acting on
is a positive self-adjoint linear
operator acting on
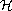 ,
,
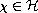 ,
and
,
and
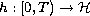 .
Using semigroup theory,
we obtain Holder continuous dependence for the control
problem generated by the method of quasireversibility.
.
Using semigroup theory,
we obtain Holder continuous dependence for the control
problem generated by the method of quasireversibility.
Published September 25, 2010.
Math Subject Classifications: 47A52, 35R25, 35A35.
Key Words: Quasireversibility; ill-posed problems.
Show me the PDF file (207K),
TEX file for this article.
 |
Beth M. Campbell Hetrick
Department of Mathematics, Gettysburg College
Gettysburg, PA 17325, USA
email: bcampbel@gettysburg.edu
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
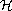 ,
the inhomogeneous ill-posed
abstract Cauchy problem is given by
,
the inhomogeneous ill-posed
abstract Cauchy problem is given by
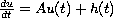 ,
,
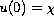 ,
,
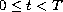 ;
where
;
where
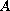 is a positive self-adjoint linear
operator acting on
is a positive self-adjoint linear
operator acting on
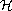 ,
,
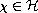 ,
and
,
and
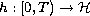 .
Using semigroup theory,
we obtain Holder continuous dependence for the control
problem generated by the method of quasireversibility.
.
Using semigroup theory,
we obtain Holder continuous dependence for the control
problem generated by the method of quasireversibility.
