2014 Madrid Conference on Applied Mathematics in honor of Alfonso Casal,
Electron. J. Diff. Eqns., Conference 22 (2015), pp. 31-45.
An application of shape differentiation to the effectiveness of a steady
state reaction-diffusion problem arising in chemical engineering
Jesus Ildefonso Diaz, David Gomez-Castro
Abstract:
In applications it is common to arrive at a problem where the choice of
an optimal domain is considered. One such problem is the one associated with
the steady state reaction diffusion equation given by a semilinear elliptic
equation with a monotone nonlinearity g. In some contexts, in particular
in chemical engineering, it is common to consider the functional given by
the integral of this nonlinear term of the solution dived by the measure of
the domain
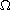 in which the pde takes place. This is often related
with the effectiveness of the reaction. In this paper our aim is to study
the differentiability of such functional as study connected to the
optimality of the best chemical reactor.
in which the pde takes place. This is often related
with the effectiveness of the reaction. In this paper our aim is to study
the differentiability of such functional as study connected to the
optimality of the best chemical reactor.
Published November 20, 2015.
Math Subject Classifications: 35J61, 46G05, 35B30.
Key Words: Shape differentiation; effectiveness factor; reaction-diffusion;
chemical engineering; numerical experiments.
Show me the PDF(825 K),
TEX and other files for this article.
 |
Jesús Ildefonso Díiaz
Departamento de Matemática Aplicada
Instituto de Matemática Interdisciplinar
Universidad Complutense de Madrid
Plaza de las Ciencias, 3, 28040 Madrid, Spain
email: jidiaz@ucm.es
|
|---|
 |
David Gómez-Castro
Instituto de Matemática Interdisciplinar and Dpto.
de Matemática Aplicada
Facultad de Ciencias Matemáticas,
Universidad Complutense de Madrid
Plaza de las Ciencias 3, 28040 Spain
email: dgcastro@ucm.es
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
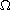 in which the pde takes place. This is often related
with the effectiveness of the reaction. In this paper our aim is to study
the differentiability of such functional as study connected to the
optimality of the best chemical reactor.
in which the pde takes place. This is often related
with the effectiveness of the reaction. In this paper our aim is to study
the differentiability of such functional as study connected to the
optimality of the best chemical reactor.

