Tenth MSU Conference on Differential Equations and Computational Simulations.
Electron. J. Diff. Eqns., Conference 23 (2016), pp. 131-138.
Existence of three solutions for a two-point singular boundary-value
problem with an unbounded weight
Dhanya Rajendran, Eunkyung Ko, Ratnasingham Shivaji
Abstract:
We show the existence of three solution for the singular
boundary-value problem
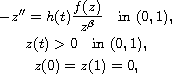
where
 ,
,
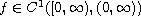 and
and
![$ h\in C((0,1], (0,\infty))$](gifs/ad.gif) is such that
is such that
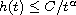 on
on
![$(0,1]$](gifs/af.gif) for some
for some
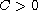 and
and
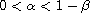 .
When there exist
two pairs of sub-supersolutions
.
When there exist
two pairs of sub-supersolutions
 and
and
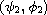 where
where
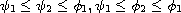 with
with
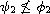 ,
and
,
and
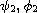 are strict sub
and super solutions. The establish the existence of at least three solutions
are strict sub
and super solutions. The establish the existence of at least three solutions
 satisfying
satisfying
![$z_1\in [\psi_1,\phi_2]$](gifs/ao.gif) ,
,
![$z_2\in [\psi_2,\phi_1]$](gifs/ap.gif) and
and
![$z_3\in [\psi_1,\phi_1]\setminus ([\psi_1,\phi_2]\cup [\psi_2,\phi_1])$](gifs/aq.gif) .
.
Published March 21, 2016.
Math Subject Classifications: 35J25, 35J55.
Key Words: Three solutions theorem; singular boundary value problems.
Show me the PDF file (215 K),
TEX file for this article.
| |
Dhanya Rajendran
Departamento de Matemática
Universidad de Concepción, Chile
email: dhanya.tr@gmail.com
|
|---|
 |
Eunkyung Ko
PDE and Functional Analysis Research Center
Department of Mathematical Sciences
Seoul National University
Seoul, 151-747, South Korea
email: ekko1115@snu.ac.kr
|
|---|
 |
Ratnasingham Shivaji
Department of Mathematics and Statistics
University of North Carolina at Greensboro
Greensboro, NC 27412, USA
email: shivaji@uncg.edu
|
Return to the table of contents
for this conference.
Return to the EJDE web page
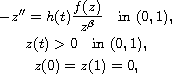
 ,
,
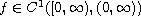 and
and
![$ h\in C((0,1], (0,\infty))$](gifs/ad.gif) is such that
is such that
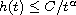 on
on
![$(0,1]$](gifs/af.gif) for some
for some
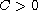 and
and
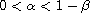 .
When there exist
two pairs of sub-supersolutions
.
When there exist
two pairs of sub-supersolutions
 and
and
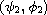 where
where
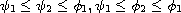 with
with
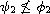 ,
and
,
and
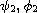 are strict sub
and super solutions. The establish the existence of at least three solutions
are strict sub
and super solutions. The establish the existence of at least three solutions
 satisfying
satisfying
![$z_1\in [\psi_1,\phi_2]$](gifs/ao.gif) ,
,
![$z_2\in [\psi_2,\phi_1]$](gifs/ap.gif) and
and
![$z_3\in [\psi_1,\phi_1]\setminus ([\psi_1,\phi_2]\cup [\psi_2,\phi_1])$](gifs/aq.gif) .
.

