Electron. J. Diff. Eqns.,
Monograph 08, 2007, (101 pages).
An algorithm for constructing Lyapunov functions
Sigurdur Freyr Hafstein
Abstract:
In this monograph we develop an algorithm for constructing Lyapunov functions for arbitrary switched dynamical systems \(\dot{\mathbf{x}} = \mathbf{f}_\sigma(t,\mathbf{x})\), possessing a uniformly asymptotically stable equilibrium. Let \(\dot{\mathbf{x}}=\mathbf{f}_p(t,\mathbf{x})\), \(p\in \mathcal{P}\), be the collection of the ODEs, to which the switched system corresponds. The number of the vector fields \(\mathbf{f}_p\) on the right-hand side of the differential equation is assumed to be finite and we assume that their components \(f_{p,i}\) are \(\mathcal{C}^2\) functions and that we can give some bounds, not necessarily close, on their second-order partial derivatives. The inputs of the algorithm are solely a finite number of the function values of the vector fields \(\mathbf{f}_p\) and these bounds. The domain of the Lyapunov function constructed by the algorithm is only limited by the size of the equilibrium's region of attraction. Note, that the concept of a Lyapunov function for the arbitrary switched system \(\dot{\mathbf{x}} = \mathbf{f}_\sigma(t,\mathbf{x})\) is equivalent to the concept of a common Lyapunov function for the systems \(\dot{\mathbf{x}}=\mathbf{f}_p(t,\mathbf{x})\), \(p\in\mathcal{P}\), and that if \(\mathcal{P}\) contains exactly one element, then the switched system is just a usual ODE \(\dot{\mathbf{x}}=\mathbf{f}(t,\mathbf{x})\). We give numerous examples of Lyapunov functions constructed by our method at the end of this monograph.
DOI: https://doi.org/10.58997/ejde.mon.08
In this monograph we develop an algorithm for constructing Lyapunov functions
for arbitrary switched dynamical systems
 ,
possessing a uniformly asymptotically stable equilibrium.
Let
,
possessing a uniformly asymptotically stable equilibrium.
Let
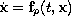 ,
,
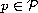 ,
be the collection of the ODEs, to which the switched system corresponds.
The number of the vector fields
,
be the collection of the ODEs, to which the switched system corresponds.
The number of the vector fields
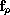 on the right-hand side
of the differential equation is assumed to be finite and we assume that
their components
on the right-hand side
of the differential equation is assumed to be finite and we assume that
their components
 are
are
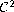 functions and that we
can give some bounds, not necessarily close, on their second-order
partial derivatives.
The inputs of the algorithm are solely a finite number of the
function values of the vector fields
functions and that we
can give some bounds, not necessarily close, on their second-order
partial derivatives.
The inputs of the algorithm are solely a finite number of the
function values of the vector fields
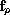 and these bounds.
The domain of the Lyapunov function constructed by the algorithm is
only limited by the size of the equilibrium's region of attraction.
Note, that the concept of a Lyapunov function for the arbitrary switched
system
and these bounds.
The domain of the Lyapunov function constructed by the algorithm is
only limited by the size of the equilibrium's region of attraction.
Note, that the concept of a Lyapunov function for the arbitrary switched
system
 is
equivalent to the concept of a common Lyapunov function for the systems
is
equivalent to the concept of a common Lyapunov function for the systems
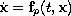 ,
,
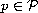 ,
and that if
,
and that if
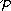 contains exactly one element, then the
switched system is just a usual ODE
contains exactly one element, then the
switched system is just a usual ODE
 .
We give numerous examples of Lyapunov functions constructed by our
method at the end of this monograph.
.
We give numerous examples of Lyapunov functions constructed by our
method at the end of this monograph.
Submitted August 29, 2006. Published August 15, 2007.
Math Subject Classifications: 35J20, 35J25.
Key Words: Lyapunov functions; switched systems; converse theorem;
piecewise affine functions.
Show me the
PDF file (6694 KB),
TEX file, and other files for this article.
 |
Sigurdur Freyr Hafstein
School of Science and Engineering
Reykjavik University
Reykjavik, Iceland
email: sigurdurh@ru.is
|
|---|
Return to the EJDE web page
 ,
possessing a uniformly asymptotically stable equilibrium.
Let
,
possessing a uniformly asymptotically stable equilibrium.
Let
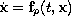 ,
,
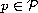 ,
be the collection of the ODEs, to which the switched system corresponds.
The number of the vector fields
,
be the collection of the ODEs, to which the switched system corresponds.
The number of the vector fields
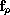 on the right-hand side
of the differential equation is assumed to be finite and we assume that
their components
on the right-hand side
of the differential equation is assumed to be finite and we assume that
their components
 are
are
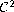 functions and that we
can give some bounds, not necessarily close, on their second-order
partial derivatives.
The inputs of the algorithm are solely a finite number of the
function values of the vector fields
functions and that we
can give some bounds, not necessarily close, on their second-order
partial derivatives.
The inputs of the algorithm are solely a finite number of the
function values of the vector fields
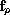 and these bounds.
The domain of the Lyapunov function constructed by the algorithm is
only limited by the size of the equilibrium's region of attraction.
Note, that the concept of a Lyapunov function for the arbitrary switched
system
and these bounds.
The domain of the Lyapunov function constructed by the algorithm is
only limited by the size of the equilibrium's region of attraction.
Note, that the concept of a Lyapunov function for the arbitrary switched
system
 is
equivalent to the concept of a common Lyapunov function for the systems
is
equivalent to the concept of a common Lyapunov function for the systems
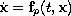 ,
,
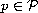 ,
and that if
,
and that if
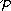 contains exactly one element, then the
switched system is just a usual ODE
contains exactly one element, then the
switched system is just a usual ODE
 .
We give numerous examples of Lyapunov functions constructed by our
method at the end of this monograph.
.
We give numerous examples of Lyapunov functions constructed by our
method at the end of this monograph.
