Electron. J. Diff. Eqns.,
Vol. 1994(1994), No. 02, pp. 1-17. Published March 15, 1994.
Large Time Behavior of Solutions to a Class of Doubly
Nonlinear Parabolic Equations
Juan J. Manfredi & Vincenzo Vespri
Abstract:
We study the large time asymptotic behavior of
solutions of the doubly degenerate parabolic equation
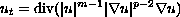
in a cylinder
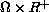 ,
with initial condition
,
with initial condition
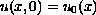 in
in
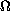 and vanishing on the parabolic boundary
and vanishing on the parabolic boundary
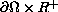 .
Here
.
Here
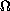 is a bounded domain in
is a bounded domain in
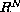 , the exponents
m and p satisfy
, the exponents
m and p satisfy
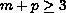 ,
,
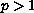 , and the
initial datum
, and the
initial datum
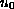 is in
is in
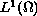 .
.
Submitted October 25, 1993. Published March 15, 1994.
Math Subject Classification: 35K65, 35K55.
Key Words: Doubly nonlinear parabolic equations, asymptotic behavior.
Show me the
PDF file (257 KB),
TEX file for this article.
Juan J. Manfredi
Department of Mathematics,
University of Pittsburgh,
Pittsburgh, PA 15260, USA
e-mail: manfredi+@pitt.edu
Vincenzo Vespri
Universita di Pavia,
Dipartimento di Matematica,
Via Abbiategrasso 209,
27100 Pavia, ITALY
e-mail: vespri@vmimat.mat.unimi.it
Return to the EJDE home page.
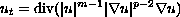
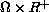 ,
with initial condition
,
with initial condition
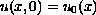 in
in
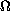 and vanishing on the parabolic boundary
and vanishing on the parabolic boundary
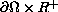 .
Here
.
Here
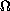 is a bounded domain in
is a bounded domain in
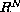 , the exponents
, the exponents
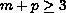 ,
,
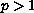 , and the
initial datum
, and the
initial datum
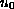 is in
is in
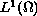 .
.