The final value problem,
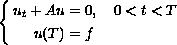
with positive self-adjoint unbounded
 . We show that the approximate problems are well posed and
that their solutions
. We show that the approximate problems are well posed and
that their solutions
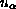 converge on
converge on
Gordon W. Clark & Seth F. Oppenheimer
Abstract:
The final value problem,
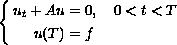
with positive self-adjoint unbounded  . We show that the approximate problems are well posed and
that their solutions
. We show that the approximate problems are well posed and
that their solutions
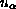 converge on
converge on
Submitted November 14, 1994. Published November 29, 1994.
Math Subject Classification: 35A35, 35R25.
Key Words: Quasireversibility, Final Value Problems, Ill-Posed Problems.
Show me the PDF file (148 KB), TEX file for this article.
Seth F. Oppenheimer
Department of Mathematics and Statistics,
Mississippi State University,
Drawer MA MSU, MS 39762, USA
e-mail: seth@math.msstate.edu