We show that if
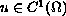 satisfies the
satisfies the
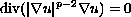
in
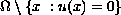 ,
then
,
then 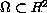 .
.
Tero Kilpelainen
Abstract:
We show that if
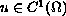 satisfies the
satisfies the
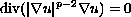
in
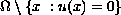 ,
then
,
then 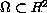 .
.
Submitted September 29, 1994.Published December 6, 1994.
Math Subject Classification: 35J60, 35B60, 31C45, 30C62.
Key Words: p-harmonic functions, p-Laplacian, removable sets.
Show me the PDF file (116 KB), TEX file for this article.