We prove existence, uniqueness and exponential decay of solutions to the mixed problem
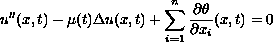
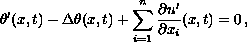
with a suitable boundary damping, and a positive real-valued function
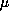 .
.
H. R. Clark , L. P. San Gil Jutuca, & M. Milla Miranda
Abstract:
We prove existence, uniqueness and exponential decay of solutions to the mixed
problem
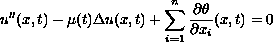
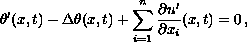
with a suitable boundary damping, and a positive real-valued function
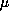 .
.
Submitted August 24, 1997. Published February 13, 1998.
Math Subject Classification: 35F15, 35N10, 35B40.
Key Words: Mixed problem, Boundary damping, Exponential stability.
Show me the PDF file (201 KB), TEX file for this article.
 |
H. R. Clark Universidade Federal Fluminense, RJ, Brazil e-mail: ganhrc@vm.uff.br |
| L. P. San Gil Jutuca Universidade do Rio de Janeiro, RJ, Brazil e-mail: rsangil@iq.ufrj.br | |
| M. Milla Miranda Universidade Federal do Rio de Janeiro, RJ, Brazil; Instituto de Matematica; CP 68530 - CEP 21949-900 |
Return to the EJDE home page