We study the nonlinear elliptic boundary value problem
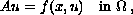
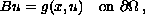
where A is an operator of p-Laplacian type,
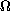 is an unbounded domain in
is an unbounded domain in
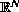 with non-compact boundary, and
f and g are subcritical nonlinearities.
We show existence of a nontrivial nonnegative weak solution
when both f and g are superlinear. Also we show
existence of at least two nonnegative solutions when one of the two
functions f, g is sublinear and the other one superlinear.
The proofs are based on variational methods applied to weighted
function spaces.
with non-compact boundary, and
f and g are subcritical nonlinearities.
We show existence of a nontrivial nonnegative weak solution
when both f and g are superlinear. Also we show
existence of at least two nonnegative solutions when one of the two
functions f, g is sublinear and the other one superlinear.
The proofs are based on variational methods applied to weighted
function spaces.
