Electron. J. Diff. Eqns., Vol. 1998(1998), No. 12, pp. 1-9.
Pressure conditions for the local regularity of solutions
of the Navier-Stokes equations
Mike O'Leary
Abstract:
We obtain a relationship between the integrability of the pressure
gradient and the the integrability of the velocity for local solutions
of the Navier--Stokes equations with finite energy. In particular, we show that
if the pressure gradient is sufficiently integrable, then the corresponding
velocity is locally bounded and smooth in the spatial variables. The result
is proven by using De Giorgi type estimates in
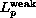 spaces.
spaces.
Submitted January 26, 1998. Published May 13, 1998.
Math Subject Classification: 35Q30, 76D05.
Key Words: Navier-Stokes, regularity, pressure.
Show me the
PDF file (134 KB),
TEX file for this article.
Mike O'Leary
Department of Mathematics, University of California Santa Cruz
Santa Cruz, CA 95064 USA.
e-mail: oleary@cats.ucsc.edu
Return to the EJDE home page
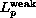 spaces.
spaces.