Electron. J. Diff. Eqns., Vol. 1998(1998), No. 16, pp. 1-10.
Quasi-geostrophic type equations with weak initial data
Jiahong Wu
Abstract:
We study the initial value problem for the quasi-geostrophic type equations
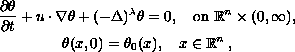
where
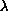 , (
, (
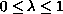 ) is a fixed parameter and
) is a fixed parameter and
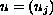 is divergence free and determined from
is divergence free and determined from
 through the Riesz transform
through the Riesz transform
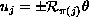 , with
, with
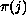 a permutation of
a permutation of
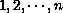 .
The initial data
.
The initial data
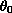 is taken
in the Sobolev space
is taken
in the Sobolev space
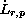 with
negative indices.
We prove local well-posedness when
with
negative indices.
We prove local well-posedness when
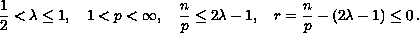
We also prove that the solution is global if
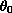 is
sufficiently small.
is
sufficiently small.
Submitted November 26, 1996. Published June 12, 1998.
Math Subject Classification: 35K22, 35Q35, 76U05.
Key Words: Quasi-geostrophic equations, Weak data, Well-posedness.
Show me the
PDF file (148 KB),
TEX file for this article.
Jiahong Wu
School of Mathematics, Institute for Advanced Study
Princeton, NJ 08540. USA
e-mail: jiahong@math.utexas.edu
Return to the EJDE home page
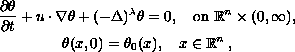
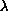 , (
, (
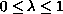 ) is a fixed parameter and
) is a fixed parameter and
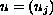 is divergence free and determined from
is divergence free and determined from
 through the Riesz transform
through the Riesz transform
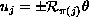 , with
, with
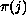 a permutation of
a permutation of
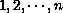 .
The initial data
.
The initial data
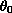 is taken
in the Sobolev space
is taken
in the Sobolev space
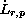 with
negative indices.
We prove local well-posedness when
with
negative indices.
We prove local well-posedness when
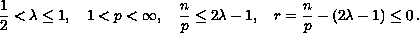
 is
sufficiently small.
is
sufficiently small.