Electron. J. Diff. Eqns., Vol. 1998(1998), No. 34, pp. 1-12.
Symmetry and convexity of level sets of solutions to
infinity Laplace's equation
Edi Rosset
Abstract:
We consider the Dirichlet problem
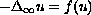 in
in
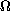 ,
,
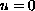 on
on
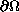
where
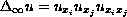 and
f is a nonnegative continuous function.
We investigate whether the solutions to this equation
inherit geometrical properties from the domain
and
f is a nonnegative continuous function.
We investigate whether the solutions to this equation
inherit geometrical properties from the domain
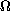 .
We obtain results concerning convexity of level sets
and symmetry of solutions.
.
We obtain results concerning convexity of level sets
and symmetry of solutions.
Submitted July 23, 1998. Published December 9, 1998.
Math Subject Classification: 35J70, 35B05.
Key Words: Infinity-Laplace equation, p-Laplace equation.
Show me the
PDF file (140K),
TEX file for this article.
 |
Edi Rosset
Dipartimento di Scienze Matematiche
Universita degli Studi di Trieste
34100 Trieste, Italy
e-mail: rossedi@univ.trieste.it |
Return to the EJDE web page
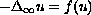 in
in
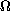 ,
,
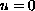 on
on
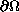
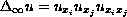 and
f is a nonnegative continuous function.
We investigate whether the solutions to this equation
inherit geometrical properties from the domain
and
f is a nonnegative continuous function.
We investigate whether the solutions to this equation
inherit geometrical properties from the domain
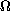 .
We obtain results concerning convexity of level sets
and symmetry of solutions.
.
We obtain results concerning convexity of level sets
and symmetry of solutions. 