In this paper we consider fully nonlinear elliptic equations, including the Monge-Ampere equation and the Weingarden equation. We assume that
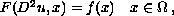
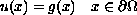
has a solution
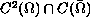 , and
, and 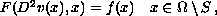
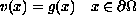
has a solution
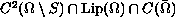 .
.
We prove that under certain conditions on
Lihe Wang & Ning Zhu
Abstract:
In this paper we consider fully nonlinear elliptic equations,
including the Monge-Ampere equation and the Weingarden equation.
We assume that
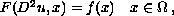
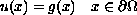
has a solution 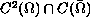 , and
, and
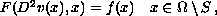
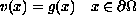
has a solution 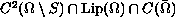 .
.
We prove that under certain conditions on
Submitted March 17, 1998. Published February 17, 1999.
Math Subject Classification: 35B65
Key Words: Nonlinear PDE, Monge-Ampere Equation, Removable singularity.
Show me the PDF file (100K), TEX file for this article.
Ning Zhu
Department of Mathematics, Suzhou University
Suzhou 215006, China