Electron. J. Diff. Eqns., Vol. 1999(1999), No. 23, pp. 1-25.
On the Dirichlet problem for quasilinear elliptic second order
equations with triple degeneracy and singularity in a domain with
a boundary conical point
Michail Borsuk & Dmitriy Portnyagin
Abstract:
In this article we prove boundedness and Holder
continuity of weak solutions to the Dirichlet problem for a second
order quasilinear elliptic equation with triple degeneracy and
singularity. In particular, we study equations of the form
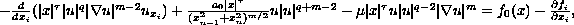
with
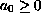 ,
,
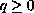 ,
,
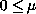 < 1, 1 <
< 1, 1 <
 , and
, and
 > m-n
in a domain with a boundary conical point. We obtain the exact
Holder exponent of the solution near the conical point.
> m-n
in a domain with a boundary conical point. We obtain the exact
Holder exponent of the solution near the conical point.
Submitted April 23, 1999. Published June 24, 1999.
Math Subject Classification: 35B45, 35B65, 35D10, 35J25, 35J60, 35J65, 35J70.
Key Words: quasilinear elliptic degenerate equations,
barrier functions, conical points.
Show me the
PDF file (245K),
TEX file for this article.
Note This article is related to another article published by EJDE.
Michail Borsuk & Dmitriy Portnyagin,
Barriers on cones for degenerate quasilinear elliptic operators,
Vol. 1998(1998), No. 11, pp. 1-8.
 |
Michail Borsuk
Department of Applied Mathematics
Olsztyn University of Agriculture and Technology
10-957 Olsztyn-Kortowo, Poland
e-mail: borsuk@art.olsztyn.pl
|
 |
Dmitriy Portnyagin
Department of Physics,
Lvov State University
290602 Lvov, Ukraine
e-mail: mitport@hotmail.com
|
Return to the EJDE web page
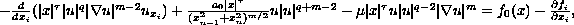
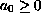 ,
,
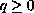 ,
,
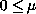 < 1, 1 <
< 1, 1 <
 , and
, and
 > m-n
in a domain with a boundary conical point. We obtain the exact
Holder exponent of the solution near the conical point.
> m-n
in a domain with a boundary conical point. We obtain the exact
Holder exponent of the solution near the conical point. 
