We consider the functional
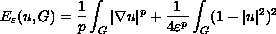
with
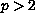 and
and
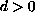 ,
on the class of functions
,
on the class of functions
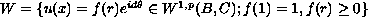 .
The location of the zeroes of the minimizer and its convergence as
.
The location of the zeroes of the minimizer and its convergence as
 approaches zero are established.
approaches zero are established.
Yutian Lei, Zhuoqun Wu, & Hongjun Yuan
Abstract:
We consider the functional
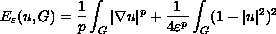
with
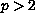 and
and
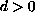 ,
on the class of functions
,
on the class of functions
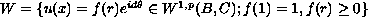 .
The location of the zeroes of the minimizer and its convergence as
.
The location of the zeroes of the minimizer and its convergence as
 approaches zero are established.
approaches zero are established.
Submitted June 8, 1999. Published September 9, 1999.
Math Subject Classifications: 35J70
Key Words: Ginzburg-Landau functional, radial functional, zeros of a minimizer.
Show me the PDF file (205K), TEX file for this article.