Electron. J. Diff. Eqns., Vol. 1999(1999), No. 37, pp. 1-20.

Dini-Campanato spaces and applications to nonlinear elliptic equations

Jay Kovats

Abstract:
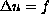We generalize a result due to Campanato [C] and use this to obtain regularity results for classical solutions of fully nonlinear elliptic equations. We demonstrate this technique in two settings. First, in the simplest setting of Poisson's equation $\Delta u=f$ in B, where f is Dini continuous in B, we obtain known estimates on the modulus of continuity of second derivatives D2u in a way that does not depend on either differentiating the equation or appealing to integral representations of solutions. Second, we use this result in the concave, fully nonlinear setting F(D2u,x)=f(x) to obtain estimates on the modulus of continuity of D2u when the Ln averages of f satisfy the Dini condition.

Submitted January 6, 1999. Revised July 19, 1999. Published September 25, 1999.
Math Subject Classifications: 35B65, 41A10.
Key Words: Fully nonlinear elliptic equations, polynomial approximation, Dini condition.

Show me the PDF file (226K), TEX file, and other files for this article.

Jay Kovats
Department of Mathematical Sciences
Florida Institute of Technology
Melbourne, FL 32901, USA
e-mail address: jkovats@zach.fit.edu
Return to the EJDE web page