We study the time-independent Schrodinger equation with radially symmetric potential
 ,
,
 ,
,
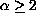 on a bounded domain
on a bounded domain
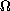 in
in
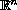 ,
,
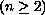 with Dirichlet boundary conditions.
In particular, we compare the eigenvalue
with Dirichlet boundary conditions.
In particular, we compare the eigenvalue
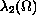 of
the operator
of
the operator
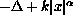 on
on
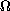 with the eigenvalue
with the eigenvalue
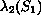 of the same operator
of the same operator
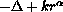 on a ball
on a ball 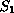 ,
where
,
where
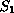 has radius such
that the first eigenvalues are the same,
has radius such
that the first eigenvalues are the same,
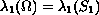 .
The main result is to show
.
The main result is to show
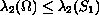 .
We also give an extension of the main
result to the case of a more general elliptic eigenvalue problem
on a bounded domain with Dirichlet boundary conditions.
.
We also give an extension of the main
result to the case of a more general elliptic eigenvalue problem
on a bounded domain with Dirichlet boundary conditions. 