Electron. J. Diff. Eqns., Vol. 2000(2000), No. 15, pp. 1-11.
A diffusion equation for composite materials
Mohamed El Hajji
Abstract:
In this article, we study the asymptotic behavior of solutions to
the diffusion equation with non-homogeneous Neumann boundary conditions.
This equation models a composite material that occupies a perforated
domain, in
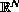 ,
with small holes whose sizes are measured by a number
,
with small holes whose sizes are measured by a number
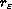 .
We examine the case when
.
We examine the case when
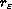 <
<
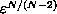 with
zero-average data around the holes, and the case when
with
zero-average data around the holes, and the case when
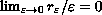 with
nonzero-average data.
with
nonzero-average data.
Submitted October 14, 1999. Published February 22, 2000.
Math Subject Classifications: 31C40, 31C45, 60J50, 31C35, 31B35.
Key Words: Diffusion equation, composite material,
asymptotic behavior, H0-convergence.
Show me the
PDF file (143K),
TEX file for this article.
 |
Mohamed El Hajji
Universite de Rouen, UFR des Sciences
UPRES-A 60 85 (Labo de Math.)
76821 Mont Saint Aignan, France
e-mail address: Mohamed.Elhajji@univ-rouen.fr
|
Return to the EJDE web page
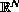 ,
with small holes whose sizes are measured by a number
,
with small holes whose sizes are measured by a number
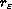 .
We examine the case when
.
We examine the case when
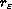 <
<
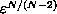 with
zero-average data around the holes, and the case when
with
zero-average data around the holes, and the case when
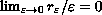 with
nonzero-average data.
with
nonzero-average data. 