Electron. J. Diff. Eqns., Vol. 2000(2000), No. 24, pp. 1-16.
Periodic and almost periodic solutions for multi-valued differential
equations in Banach spaces
E. Hanebaly & B. Marzouki
Abstract:
It is known that for
 -periodic
differential
equations of monotonous type, in uniformly convex Banach spaces,
the existence of a bounded solution on
-periodic
differential
equations of monotonous type, in uniformly convex Banach spaces,
the existence of a bounded solution on
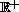 is equivalent to the existence of an
is equivalent to the existence of an
 -periodic
solution (see Haraux [5] and
Hanebaly [7, 10]). It is also known that if the Banach space
is strictly convex and the equation is almost periodic and of
monotonous type, then the existence of a continuous solution with
a precompact range is equivalent to the existence of an almost
periodic solution (see Hanebaly [8]).
In this note we want to generalize the results above for multi-valued
differential equations.
-periodic
solution (see Haraux [5] and
Hanebaly [7, 10]). It is also known that if the Banach space
is strictly convex and the equation is almost periodic and of
monotonous type, then the existence of a continuous solution with
a precompact range is equivalent to the existence of an almost
periodic solution (see Hanebaly [8]).
In this note we want to generalize the results above for multi-valued
differential equations.
Submitted July 16, 1999. Published March 30, 2000.
Math Subject Classifications: 34A60, 34C25, 34C27, 47H10.
Key Words: Multi-valued differential equation, Hyper-accretive,
Almost periodicity, Banach space.
Show me the
PDF file (169K),
TEX file for this article.
E. Hanebaly
Universite Mohammed V Faculte des Sciences
Departement de Mathematiques, Rabat, Maroc.
e-mail: hanebaly@fsr.ac.ma
Brahim Marzouki
Universite Mohammed I Faculte des Sciences
Departement de Mathematiques, Oujda, Maroc.
e-mail: marzouki@sciences.univ-oujda.ac.ma
Return to the EJDE web page
 -periodic
differential
equations of monotonous type, in uniformly convex Banach spaces,
the existence of a bounded solution on
-periodic
differential
equations of monotonous type, in uniformly convex Banach spaces,
the existence of a bounded solution on
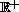 is equivalent to the existence of an
is equivalent to the existence of an
 -periodic
solution (see Haraux [5] and
Hanebaly [7, 10]). It is also known that if the Banach space
is strictly convex and the equation is almost periodic and of
monotonous type, then the existence of a continuous solution with
a precompact range is equivalent to the existence of an almost
periodic solution (see Hanebaly [8]).
In this note we want to generalize the results above for multi-valued
differential equations.
-periodic
solution (see Haraux [5] and
Hanebaly [7, 10]). It is also known that if the Banach space
is strictly convex and the equation is almost periodic and of
monotonous type, then the existence of a continuous solution with
a precompact range is equivalent to the existence of an almost
periodic solution (see Hanebaly [8]).
In this note we want to generalize the results above for multi-valued
differential equations.