Electron. J. Diff. Eqns., Vol. 2000(2000), No. 40, pp. 1-15.
Three symmetric positive solutions for Lidstone problems by a
generalization of the Leggett-Williams theorem
Richard I. Avery, John M. Davis, & Johnny Henderson
Abstract:
We study the existence of solutions to the fourth order Lidstone
boundary value problem
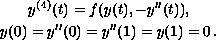
By imposing growth conditions on
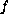 and using a generalization of the
multiple fixed point theorem by Leggett and Williams, we show
the existence of at least three symmetric positive solutions.
We also prove analogous results for difference equations.
and using a generalization of the
multiple fixed point theorem by Leggett and Williams, we show
the existence of at least three symmetric positive solutions.
We also prove analogous results for difference equations.
Submitted December 6, 1999. Published May 23, 2000.
Math Subject Classifications: 34B18, 34B27, 39A12, 39A99.
Key Words: Lidstone boundary value problem, Green's function,
multiple solutions, fixed points, difference equation.
Show me the
PDF file (155K),
TEX file for this article.
 |
Richard I. Avery
College of Natural Sciences,
Dakota State University
Madison, SD 57042, USA
email: averyr@pluto.dsu.edu |
 |
John M. Davis
Department of Mathematics,
Baylor University
Waco, TX 76798, USA
email: John_M_Davis@baylor.edu |
 |
Johnny Henderson
Department of Mathematics,
Auburn University
Auburn, AL 36849, USA
email: hendej2@mail.auburn.edu
email: Johnny_Henderson@baylor.edu
|
Return to the EJDE web page
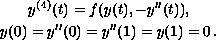
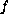 and using a generalization of the
multiple fixed point theorem by Leggett and Williams, we show
the existence of at least three symmetric positive solutions.
We also prove analogous results for difference equations.
and using a generalization of the
multiple fixed point theorem by Leggett and Williams, we show
the existence of at least three symmetric positive solutions.
We also prove analogous results for difference equations. 

