Electron. J. Diff. Eqns., Vol. 2000(2000), No. 47, pp. 1-19.
Stochastic perturbations of the Allen-Cahn equation
Tony Shardlow
Abstract:
Consider the Allen-Cahn equation with small diffusion
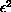 perturbed by a space time white noise of intensity
perturbed by a space time white noise of intensity
 . In the
limit,
. In the
limit,
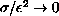 , solutions converge to
the noise free problem in the
, solutions converge to
the noise free problem in the
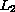 norm.
Under these conditions,
asymptotic results for the evolution of phase boundaries in the
deterministic setting are extended, to describe the behaviour of the
stochastic Allen-Cahn PDE by a system of stochastic differential
equations. Computations are described, which support the
asymptotic derivation.
norm.
Under these conditions,
asymptotic results for the evolution of phase boundaries in the
deterministic setting are extended, to describe the behaviour of the
stochastic Allen-Cahn PDE by a system of stochastic differential
equations. Computations are described, which support the
asymptotic derivation.
Submitted April 18, 2000. Published June 15, 2000.
Math Subject Classifications: 60H15, 74N20, 45M05.
Key Words: dynamics of phase-boundaries, stochastic partial
differential equations, asymptotics.
Show me the
PDF file (411K),
TEX file for this article.
Tony Shardlow
Dept. Computer Science
University of Manchester
Oxford Road
Manchester M13 9PL, England
e-amil: shardlow@bioinf.man.ac.uk
Return to the EJDE web page
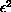 perturbed by a space time white noise of intensity
perturbed by a space time white noise of intensity
 . In the
limit,
. In the
limit,
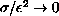 , solutions converge to
the noise free problem in the
, solutions converge to
the noise free problem in the
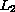 norm.
Under these conditions,
asymptotic results for the evolution of phase boundaries in the
deterministic setting are extended, to describe the behaviour of the
stochastic Allen-Cahn PDE by a system of stochastic differential
equations. Computations are described, which support the
asymptotic derivation.
norm.
Under these conditions,
asymptotic results for the evolution of phase boundaries in the
deterministic setting are extended, to describe the behaviour of the
stochastic Allen-Cahn PDE by a system of stochastic differential
equations. Computations are described, which support the
asymptotic derivation.