Electron. J. Diff. Eqns., Vol. 2000(2000), No. 52, pp. 1-42.
Multiplicity results for classes of one-dimensional p-Laplacian
boundary-value problems with cubic-like nonlinearities
Idris Addou
Abstract:
We study boundary-value problems of the type
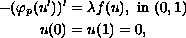
where p>1,
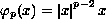 , and
, and
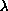 is positive. We provide multiplicity results when f behaves like
a cubic with three distinct roots, at which it satisfies Lipschitz-type
conditions involving a parameter q>1. We shall show how changes in the
position of q with respect to p lead to different behavior of the
solution set. When dealing with sign-changing solutions, we assume
that f is half-odd; a condition generalizing the usual oddness.
We use a quadrature method.
is positive. We provide multiplicity results when f behaves like
a cubic with three distinct roots, at which it satisfies Lipschitz-type
conditions involving a parameter q>1. We shall show how changes in the
position of q with respect to p lead to different behavior of the
solution set. When dealing with sign-changing solutions, we assume
that f is half-odd; a condition generalizing the usual oddness.
We use a quadrature method.
Submitted April 16, 1999. Revised May 1, 2000. Published July 3, 2000.
Math Subject Classifications: 34B15.
Key Words: p-Laplacian, time-maps, multiplicity results,
cubic-like nonlinearities.
Show me the
PDF file (312K),
TEX file for this article.
 |
Idris Addou
USTHB, Institut de Mathematiques
El-Alia, B.P. no. 32 Bab-Ezzouar
16111, Alger, Algerie.
e-mail: idrisaddou@hotmail.com |
Return to the EJDE web page
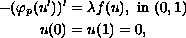
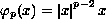 , and
, and
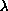 is positive. We provide multiplicity results when f behaves like
a cubic with three distinct roots, at which it satisfies Lipschitz-type
conditions involving a parameter q>1. We shall show how changes in the
position of q with respect to p lead to different behavior of the
solution set. When dealing with sign-changing solutions, we assume
that f is half-odd; a condition generalizing the usual oddness.
We use a quadrature method.
is positive. We provide multiplicity results when f behaves like
a cubic with three distinct roots, at which it satisfies Lipschitz-type
conditions involving a parameter q>1. We shall show how changes in the
position of q with respect to p lead to different behavior of the
solution set. When dealing with sign-changing solutions, we assume
that f is half-odd; a condition generalizing the usual oddness.
We use a quadrature method. 