This paper studies the spatially periodic incompressible fluid motion in
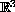 excited by the external force
excited by the external force
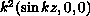 with
with
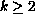 an integer.
This driving force gives rise to the existence of the
unidirectional basic steady flow
an integer.
This driving force gives rise to the existence of the
unidirectional basic steady flow
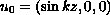 for any Reynolds number. It is shown in Theorem 1.1 that there exist a
number of critical Reynolds numbers such that
for any Reynolds number. It is shown in Theorem 1.1 that there exist a
number of critical Reynolds numbers such that
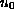 bifurcates
into either 4 or 8 or 16 different steady states, when the Reynolds number
increases across each of such numbers.
bifurcates
into either 4 or 8 or 16 different steady states, when the Reynolds number
increases across each of such numbers. Thanks to the Rabinowitz global bifurcation theorem, all of the bifurcation solutions are extended to global branches for
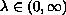 .
Moreover we prove that when
.
Moreover we prove that when
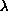 passes each critical value, a) all the
corresponding global branches do not intersect with the trivial branch
passes each critical value, a) all the
corresponding global branches do not intersect with the trivial branch
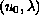 ,
and b) some of them never intersect each other; see Theorem 1.2 in this article.
,
and b) some of them never intersect each other; see Theorem 1.2 in this article.