Electron. J. Diff. Eqns., Vol. 2000(2000), No. 65, pp. 1-8.
Positive solutions to a second order multi-point boundary-value problem
Daomin Cao & Ruyun Ma
Abstract:
We prove the existence of positive solutions to the boundary-value problem
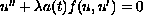
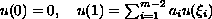 ,
,
where
 is a continuous function that may change sign on [0,1],
is a continuous function that may change sign on [0,1],
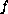 is a continuous function with
is a continuous function with
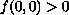 , and
, and
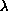 is a samll
positive constant. For finding solutions we use the Leray-Schauder
fixed point theorem.
is a samll
positive constant. For finding solutions we use the Leray-Schauder
fixed point theorem.
Submitted September 18, 2000. Published October 30, 2000.
Math Subject Classifications: 34B10.
Key Words: Multi-point boundary value problem, positive solution,
fixed point theorem.
Show me the
PDF file (108K),
TEX file for this article.
 |
Daomin Cao
Institute of Applied Mathematics
Academy of Mathematics and System Sciences
Beijing 100080, People's Republic of China
email: cao@amath6.amt.ac.cn |
|---|
 |
Ruyun Ma
Department of Mathematics
Northwest Normal University
Lanzhou 730070, Gansu, P. R. China
email: mary@nwnu.edu.cn |
Return to the EJDE web page
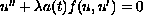
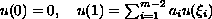 ,
, is a continuous function that may change sign on [0,1],
is a continuous function that may change sign on [0,1],
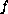 is a continuous function with
is a continuous function with
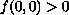 , and
, and
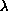 is a samll
positive constant. For finding solutions we use the Leray-Schauder
fixed point theorem.
is a samll
positive constant. For finding solutions we use the Leray-Schauder
fixed point theorem.

