Electron. J. Diff. Eqns., Vol. 2000(2000), No. 67, pp. 1-22.
Singular solutions of doubly singular
parabolic equations with absorption
Yuanwei Qi & Mingxin Wang
Abstract:
In this paper we study a doubly singular parabolic equation with
absorption,
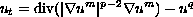
with
 ,
,
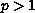 ,
,
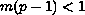 , and
, and
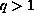 .
We give a complete classification of solutions, which we call singular,
that are non-negative, non-trivial, continuous in
.
We give a complete classification of solutions, which we call singular,
that are non-negative, non-trivial, continuous in
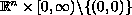 ,
and satisfy
,
and satisfy
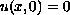 for all
for all
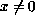 .
Applications of similar but simpler equations show that these solutions
are very important in the study of intermediate asymptotic behavior of
general solutions.
.
Applications of similar but simpler equations show that these solutions
are very important in the study of intermediate asymptotic behavior of
general solutions.
Submitted July 15, 2000. Published November 8, 2000.
Math Subject Classifications: 35K65, 35K15.
Key Words: doubly singular parabolic equation, absorption, singular solutions.
Show me the
PDF file (223K),
TEX file for this article.
Yuanwei Qi
Department of Mathematics
Hong Kong University of Science & Technology
Hong Kong,
email: maqi@uxmail.ust.hk
Mingxin Wang
Department of Applied Mathematics, Southeast University,
Nanjing 210018, P. R. China
email: mxwang@seu.edu.cn
Return to the EJDE web page
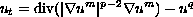
 ,
,
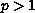 ,
,
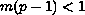 , and
, and
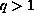 .
We give a complete classification of solutions, which we call singular,
that are non-negative, non-trivial, continuous in
.
We give a complete classification of solutions, which we call singular,
that are non-negative, non-trivial, continuous in
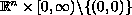 ,
and satisfy
,
and satisfy
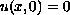 for all
for all
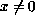 .
Applications of similar but simpler equations show that these solutions
are very important in the study of intermediate asymptotic behavior of
general solutions.
.
Applications of similar but simpler equations show that these solutions
are very important in the study of intermediate asymptotic behavior of
general solutions.