Electron. J. Diff. Eqns., Vol. 2001(2001), No. 08, pp. 1-8.
Nonsmoothing in a single conservation law with memory
G. Gripenberg
Abstract:
It is shown that, provided the nonlinearity
 is strictly convex, a discontinuity in the initial value
is strictly convex, a discontinuity in the initial value
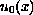 of the solution of the equation
of the solution of the equation

where
 and
and
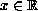 ,
is not immediately smoothed out even if the memory kernel
,
is not immediately smoothed out even if the memory kernel
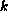 is such that the solution of the problem where
is such that the solution of the problem where
 is a linear function is continuous for
is a linear function is continuous for
 .
.
Submitted September 11, 2000. Published January 11, 2001.
Math Subject Classifications: 35L65, 35L67, 45K05.
Key Words: conservation law, discontinuous solution, memory.
Show me the
PDF file (133K),
TEX file for this article.
 |
Gustaf Gripenberg
Institute of Mathematics
Helsinki University of Technology
P.O. Box 1100, FIN-02015 HUT, Finland
e-mail: gustaf.gripenberg@hut.fi
http://www.math.hut.fi/~ggripenb
|
|---|
Return to the EJDE web page
 is strictly convex, a discontinuity in the initial value
is strictly convex, a discontinuity in the initial value
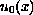 of the solution of the equation
of the solution of the equation

 and
and
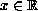 ,
is not immediately smoothed out even if the memory kernel
,
is not immediately smoothed out even if the memory kernel
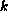 is such that the solution of the problem where
is such that the solution of the problem where
 is a linear function is continuous for
is a linear function is continuous for
 .
. 