The behaviour of dynamics at infinity has not received much attention, even though it was central to Poincare's analysis of qualitative dynamics. Poincare's `sphere' is actually a projective plane and our treatment of dynamics at infinity in more than two dimensions requires the use of
.
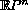In control theory, `strange' transients have been reported
by Kokotovic and Sussmann, where they go by the name of
`peaking behaviour'.
These have a simple explanation when we consider the dynamics
on the Poincare compactification of state space.
In this work, we propose to give an analysis of
the issues arising in trying to examine the dynamics at infinite
radius for dynamical systems in arbitrary dimension.
Use is made of the Newton polytope and of recent results on
principal parts of vector fields.
