We consider the eigenvalue problem
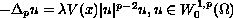
where
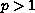 ,
,
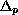 is the p-Laplacian operator,
is the p-Laplacian operator,
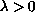 ,
,
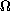 is a bounded domain in
is a bounded domain in
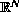 and
and
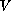 is a given function in
is a given function in
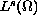 (
(
 depending on
depending on
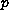 and
and
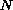 ).
The weight function
).
The weight function
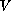 may change sign and has nontrivial positive part.
We prove that the least positive eigenvalue is simple, isolated in the
spectrum and it is the unique eigenvalue associated to a nonnegative
eigenfunction. Furthermore, we prove the strict monotonicity of the
least positive eigenvalue with respect to the domain and the weight.
may change sign and has nontrivial positive part.
We prove that the least positive eigenvalue is simple, isolated in the
spectrum and it is the unique eigenvalue associated to a nonnegative
eigenfunction. Furthermore, we prove the strict monotonicity of the
least positive eigenvalue with respect to the domain and the weight.
