Electron. J. Diff. Eqns., Vol. 2001(2001), No. 35, pp. 1-15.
Some observations on the first eigenvalue of the p-Laplacian and
its connections with asymmetry
Tilak Bhattacharya
Abstract:
In this work, we present a lower bound for the first eigenvalue
of the p-Laplacian on bounded domains in
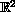 .
Let
.
Let
 be the first eigenvalue and
be the first eigenvalue and
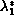 be the first eigenvalue
for the ball of the same volume. Then we show that
be the first eigenvalue
for the ball of the same volume. Then we show that
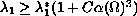 , for some constant
, for some constant
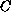 ,
where
,
where
 is the asymmetry of the domain
is the asymmetry of the domain
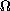 .
This provides a
lower bound sharper than the bound in Faber-Krahn inequality.
.
This provides a
lower bound sharper than the bound in Faber-Krahn inequality.
Submitted September 3, 2000. Published May 16, 2001.
Math Subject Classifications: 35J60, 35P30.
Key Words: Asymmetry, De Giorgi perimeter, p-Laplacian,
first eigenvalue, Talenti's inequality.
Show me the
PDF file (261K),
TEX file for this article.
 |
Tilak Bhattacharya
Indian Statistical Institute
7, S.J.S. Sansanwal Marg
New Delhi 110 016 India
e-mail: tlk@isid.isid.ac.in |
Current address:
Mathematics Department, Central Michigan University
Mount Pleasant, MI 48859 USA
e-mail: hadronT@netscape.net
Return to the EJDE web page
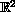 .
Let
.
Let
 be the first eigenvalue and
be the first eigenvalue and
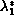 be the first eigenvalue
for the ball of the same volume. Then we show that
be the first eigenvalue
for the ball of the same volume. Then we show that
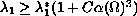 , for some constant
, for some constant
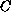 ,
where
,
where
 is the asymmetry of the domain
is the asymmetry of the domain
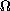 .
This provides a
lower bound sharper than the bound in Faber-Krahn inequality.
.
This provides a
lower bound sharper than the bound in Faber-Krahn inequality.
