We study the Melnikov function associated with a periodic perturbation of a differential equation having a homoclinic orbit. Our main interest is the characterization of perturbations that give rise to vanishing or non-vanishing of the Melnikov function. For this purpose we show that, in some cases, the Fourier coefficients of the Melkinov function can be evaluated by means of the calculus of residues. We apply this result, among other things, to the construction of a second-order equation whose Melnikov function vanishes identically for any
 ,
,
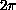 -periodic
perturbation. Then we study the second
order Melnikov function of the perturbed equation, and prove it is
non-vanishing for a large class of perturbations.
-periodic
perturbation. Then we study the second
order Melnikov function of the perturbed equation, and prove it is
non-vanishing for a large class of perturbations.

