 -biharmonic equations
-biharmonic equations
 -biharmonic equations
-biharmonic equations
Jiri Benedikt
Abstract:
The goal of this paper is to prove existence and uniqueness
of a solution of the initial value problem for the equation
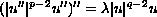
where
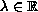 and
and
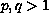 .
We prove the existence for
.
We prove the existence for
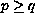 only, and give a
counterexample which shows that for
only, and give a
counterexample which shows that for
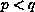 there need not exist
a global solution (blow-up of the solution can occur).
On the other hand, we prove the uniqueness for
there need not exist
a global solution (blow-up of the solution can occur).
On the other hand, we prove the uniqueness for
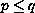 ,
and show that for
,
and show that for
 the uniqueness does not hold true
(we give a corresponding counterexample again).
Moreover, we deal with continuous dependence of the solution on
the initial conditions and parameters.
the uniqueness does not hold true
(we give a corresponding counterexample again).
Moreover, we deal with continuous dependence of the solution on
the initial conditions and parameters.
An addendum was attached on July 28, 2003. In Remark 4.6, fourth line (page 15) there should be $u(t)=K(t-t_0)^r$ instead of $u(t)=K(H-t)^r$.
Submitted April 15, 2002. Published June 10, 2002.
Math Subject Classifications: 34A12, 34C11, 34L30.
Key Words: p-biharmonic operator, existence and uniqueness of solution,
continuous dependence on initial conditions, jumping nonlinearity.
Show me the PDF file (303K), TEX file for this article.
 |
Jiri Benedikt Centre of Applied Mathematics University of West Bohemia Univerzitni 22, 306 14 Plzen Czech Republic e-mail: benedikt@kma.zcu.cz |
|---|
Return to the EJDE web page