We consider, an initial-value problem for the thermal-diffusive combustion system
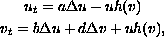
where
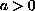 ,
,
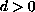 ,
,
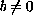 ,
,
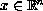 ,
,
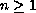 ,
with
,
with
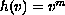 ,
,
 is an even nonnegative integer, and the
initial data
is an even nonnegative integer, and the
initial data
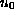 ,
,
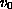 are bounded uniformly continuous and
nonnegative. It is known that by a simple comparison if
are bounded uniformly continuous and
nonnegative. It is known that by a simple comparison if
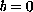 ,
,
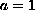 ,
,
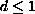 and
and
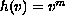 with
with
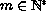 ,
the solutions are uniformly bounded in time.
When
,
the solutions are uniformly bounded in time.
When
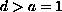 ,
,
 ,
,
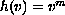 with
with
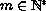 ,
Collet and Xin [2] proved the existence of global classical
solutions and showed that the
,
Collet and Xin [2] proved the existence of global classical
solutions and showed that the
 norm of
norm of
 can not
grow faster than
can not
grow faster than
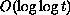 for any space dimension.
In our case, no comparison principle seems to apply.
Nevertheless using techniques form [2], we essentially prove
the existence of global classical solutions if
for any space dimension.
In our case, no comparison principle seems to apply.
Nevertheless using techniques form [2], we essentially prove
the existence of global classical solutions if
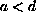 ,
,
 ,
and
,
and
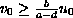 .
.
