Electron. J. Diff. Eqns., Vol. 2002(2002), No. 80, pp. 1-10.
A note on the singular Sturm-Liouville problem with infinitely
many solutions
Nickolai Kosmatov
Abstract:
We consider the Sturm-Liouville nonlinear boundary-value problem
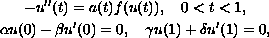
where
 ,
,
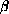 ,
,
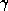 ,
,
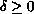 ,
,
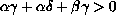 and
and
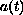 is in a class of singular functions. Using a fixed point
theorem we show that under certain growth conditions
imposed on
is in a class of singular functions. Using a fixed point
theorem we show that under certain growth conditions
imposed on
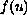 the problem admits infinitely many solutions.
the problem admits infinitely many solutions.
Submitted November 13, 2001. Published September 27, 2002.
Math Subject Classifications: 34B16, 34B18.
Key Words: Sturm-Liouville problem, Green's function,
fixed point theorem, Holder's inequality,
multiple solutions.
Show me the
PDF file (225K),
TEX file for this article.
Nickolai Kosmatov
Department of Mathematics and Statistics
University of Arkansas at Little Rock
Little Rock, Arkansas 72204-1099, USA
e-mail: nxkosmatov@ualr.edu
Return to the EJDE web page
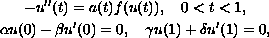
 ,
,
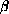 ,
,
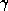 ,
,
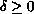 ,
,
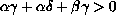 and
and
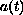 is in a class of singular functions. Using a fixed point
theorem we show that under certain growth conditions
imposed on
is in a class of singular functions. Using a fixed point
theorem we show that under certain growth conditions
imposed on
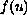 the problem admits infinitely many solutions.
the problem admits infinitely many solutions.