We study the Cauchy problem for the nonlinear (possibly strongly) degenerate parabolic transport-diffusion equation

where the coefficient
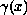 is possibly discontinuous and
is possibly discontinuous and
 is genuinely nonlinear, but not necessarily
convex or concave. Existence of a weak solution is proved by
passing to the limit as
is genuinely nonlinear, but not necessarily
convex or concave. Existence of a weak solution is proved by
passing to the limit as
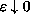 in a suitable sequence
in a suitable sequence
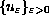 of
smooth approximations solving the problem above with the transport
flux
of
smooth approximations solving the problem above with the transport
flux
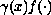 replaced by
replaced by
 and the diffusion function
and the diffusion function
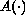 replaced by
replaced by
 ,
where
,
where
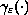 is smooth and
is smooth and
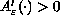 .
The main technical challenge is to deal with the fact
that the total variation
.
The main technical challenge is to deal with the fact
that the total variation
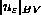 cannot be bounded uniformly in
cannot be bounded uniformly in
 ,
and hence one cannot derive directly strong convergence of
,
and hence one cannot derive directly strong convergence of
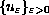 .
In the purely hyperbolic case
(
.
In the purely hyperbolic case
(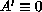 ),
where existence has already been established by a
number of authors, all existence results to date have used a
singular mapping to overcome the lack of a variation bound.
Here we derive instead strong convergence via a series of
a priori (energy) estimates that allow us to deduce convergence
of the diffusion function and use the compensated compactness
method to deal with the transport term.
),
where existence has already been established by a
number of authors, all existence results to date have used a
singular mapping to overcome the lack of a variation bound.
Here we derive instead strong convergence via a series of
a priori (energy) estimates that allow us to deduce convergence
of the diffusion function and use the compensated compactness
method to deal with the transport term.


