In this paper we study the generalized logistic equation
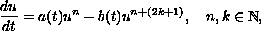
which governs the population growth of a self-limiting specie, with
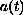 ,
,
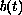 being continuous bounded functions.
We obtain a unique global, positive and bounded solution which,
further, plays the role of a frontier which clarifies the asymptotic
behavior or extensibility backwards and further it is an attractor
forward of all positive solutions. We prove also that the function
being continuous bounded functions.
We obtain a unique global, positive and bounded solution which,
further, plays the role of a frontier which clarifies the asymptotic
behavior or extensibility backwards and further it is an attractor
forward of all positive solutions. We prove also that the function
![$$
\phi (t)=\sqrt[2k+1]{a(t)/b(t)}
$$](gifs/ad.gif)
plays a fundamental role in the study of logistic equations since if it is monotone, then it is an attractor of positive solutions forward in time. Furthermore, we may relax the boundeness assumption on
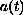 and
and
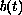 to a boundeness of it. An existence result of
a positive periodic solution is also given for the case where
to a boundeness of it. An existence result of
a positive periodic solution is also given for the case where
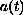 and
and
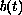 are also periodic (actually we derive a necessary
and sufficient condition for that). Our technique is a topological
one of Knesser's type (connecteness and compactness of the solutions
funnel).
are also periodic (actually we derive a necessary
and sufficient condition for that). Our technique is a topological
one of Knesser's type (connecteness and compactness of the solutions
funnel).

