Electron. J. Diff. Eqns., Vol. 2003(2003), No. 18, pp. 1-11.
Remarks on semilinear problems with nonlinearities depending on
the derivative
Jose Maria Almira & Naira Del Toro
Abstract:
In this paper, we continue some work by
Canada and Drabek [1] and Mawhin [6] on the
range of the Neumann and Periodic boundary value problems:
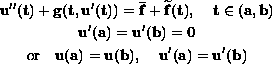
where
![$\mathbf{g}\in C([a,b]\times \mathbb{R}^{n},\mathbb{R}^n)$](gifs/ab.gif) ,
,
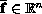 , and
, and
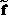 has mean value zero. For the Neumann problem
with
has mean value zero. For the Neumann problem
with
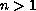 ,
we prove that for a fixed
,
we prove that for a fixed
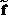 the range can
contain an infinity continuum. For the one dimensional case,
we study the asymptotic behavior of the range in both problems.
the range can
contain an infinity continuum. For the one dimensional case,
we study the asymptotic behavior of the range in both problems.
Submitted December 5, 2002. Published February 20, 2003.
Math Subject Classifications: 34B15, 34L30.
Key Words: Nonlinear boundary-value problem, Neumann and Periodic problems.
Show me the
PDF file (223K),
TEX file for this article.
 |
Jose Maria Almira
Departamento de Matematicas
Universidad de Jaen. E.U.P. Linares
C/ Alfonso X el Sabio, 28.
23700 Linares (Jaen) Spain
e-mail: jmalmira@ujaen.es |
|---|
 |
Naira Del Toro
Departamento de Matematicas
Universidad de Jaen. E.U.P. Linares
C/ Alfonso X el Sabio, 28.
23700 Linares (Jaen) Spain
e-mail: ndeltoro@ujaen.es |
|---|
Return to the EJDE web page
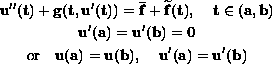
![$\mathbf{g}\in C([a,b]\times \mathbb{R}^{n},\mathbb{R}^n)$](gifs/ab.gif) ,
,
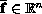 , and
, and
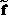 has mean value zero. For the Neumann problem
with
has mean value zero. For the Neumann problem
with
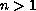 ,
we prove that for a fixed
,
we prove that for a fixed
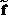 the range can
contain an infinity continuum. For the one dimensional case,
we study the asymptotic behavior of the range in both problems.
the range can
contain an infinity continuum. For the one dimensional case,
we study the asymptotic behavior of the range in both problems.

