Electron. J. Diff. Eqns., Vol. 2003(2003), No. 19, pp. 1-12.
Nonlinear singular Navier problem of fourth order
Syrine Masmoudi & Malek Zribi
Abstract:
We present an existence result for a nonlinear singular differential
equation of fourth order with Navier boundary conditions.
Under appropriate conditions on the nonlinearity
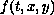 ,
we prove that the problem
,
we prove that the problem
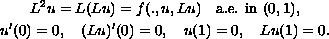
has a positive solution behaving like
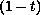 on
on
![$[0,1]$](gifs/ad.gif) .
Here
.
Here
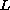 is a differential operator of second order,
is a differential operator of second order,
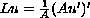 . For
. For
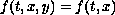 ,
we prove a
uniqueness result. Our approach is based on estimates for
Green functions and on Schauder's fixed point theorem.
,
we prove a
uniqueness result. Our approach is based on estimates for
Green functions and on Schauder's fixed point theorem.
Submitted September 29, 2002. Published February 28, 2003.
Math Subject Classifications: 34B15, 34B27.
Key Words: Nonlinear singular Navier problem, Green function,
positive solution.
Show me the
PDF file (213K),
TEX file for this article.
 |
Syrine Masmoudi
Departement de Mathematiques
Faculte des Sciences de Tunis
Campus Universitaire, 1060 Tunis, Tunisia
e-amil: Syrine.Sassi@fst.rnu.tn
|
|---|
 |
Malek Zribi
Departement de Mathematiques
Faculte des Sciences de Tunis
Campus Universitaire, 1060 Tunis, Tunisia
e-mail: Malek.Zribi@insat.rnu.tn
|
|---|
Return to the EJDE web page
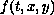 ,
we prove that the problem
,
we prove that the problem
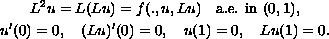
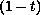 on
on
![$[0,1]$](gifs/ad.gif) .
Here
.
Here
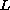 is a differential operator of second order,
is a differential operator of second order,
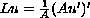 . For
. For
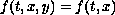 ,
we prove a
uniqueness result. Our approach is based on estimates for
Green functions and on Schauder's fixed point theorem.
,
we prove a
uniqueness result. Our approach is based on estimates for
Green functions and on Schauder's fixed point theorem.

