Electron. J. Diff. Eqns.,
Vol. 2003(2003), No. 23, pp. 1-11.
L^1 singular limit for relaxation and viscosity
approximations of extended traffic flow models
Christian Klingenberg, Yun-guang Lu, & Hui-jiang Zhao
Abstract:
This paper considers the Cauchy problem for an extended
traffic flow model with
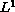 -bounded
initial data.
A solution of the corresponding equilibrium equation
with
-bounded
initial data.
A solution of the corresponding equilibrium equation
with
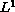 -bounded
initial data is given by the limit of
solutions of viscous approximations of the original
system as the dissipation parameter
-bounded
initial data is given by the limit of
solutions of viscous approximations of the original
system as the dissipation parameter
 tends to zero
more slowly than the response time
tends to zero
more slowly than the response time
 . The proof of
convergence is obtained by applying the Young measure to
solutions introduced by DiPerna and, based on the estimate
. The proof of
convergence is obtained by applying the Young measure to
solutions introduced by DiPerna and, based on the estimate
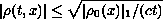
derived from one of Lax's results and Diller's idea,
the limit function
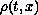 is shown to be a
is shown to be a
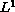 -entropy
week solution. A direct byproduct is that we can get the
existence of
-entropy
week solution. A direct byproduct is that we can get the
existence of
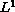 -entropy
solutions for the Cauchy problem
of the scalar conservation law with
-entropy
solutions for the Cauchy problem
of the scalar conservation law with
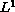 -bounded
initial data
without any restriction on the growth exponent of the flux
function provided that the flux function is strictly convex.
Our result shows that, unlike the weak solutions of the
incompressible fluid flow equations studied by DiPerna
and Majda in [6], for convex scalar conservation laws with
-bounded
initial data
without any restriction on the growth exponent of the flux
function provided that the flux function is strictly convex.
Our result shows that, unlike the weak solutions of the
incompressible fluid flow equations studied by DiPerna
and Majda in [6], for convex scalar conservation laws with
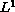 -bounded
initial data, the concentration phenomenon will
never occur in its global entropy solutions.
-bounded
initial data, the concentration phenomenon will
never occur in its global entropy solutions.
Submitted October 25, 2002. Published March 7, 2003.
Math Subject Classifications: 35B40, 35L65.
Key Words: Singular limit, traffic flow model, relaxation and
viscosity approximation.
Show me the
PDF file (221K),
TEX file for this article.
 |
Christian Klingenberg
Department of Mathematicas, Wurzburg University
Wurzburg, 97074, Germany
e-mail: klingen@mathematik.uni-wuerzburg.de |
|---|
| |
Yun-guang Lu
Department of Mathematics
University of Science and Technology of China, Hefei, China
and
Departamento de Matematicas
Universidad Nacional de Colombia, Bogota, Colombia
e-mail: yglu@matematicas.unal.edu.co |
|---|
| |
Hui-jiang Zhao
Institute of Physics and Mathematicas
Chinese Academy of Sciences, Wuhan, China
e-mail: hjzhao@wipm.whcnc.ac.cn |
|---|
Return to the EJDE web page

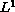 -bounded
initial data.
A solution of the corresponding equilibrium equation
with
-bounded
initial data.
A solution of the corresponding equilibrium equation
with
 tends to zero
more slowly than the response time
tends to zero
more slowly than the response time
 . The proof of
convergence is obtained by applying the Young measure to
solutions introduced by DiPerna and, based on the estimate
. The proof of
convergence is obtained by applying the Young measure to
solutions introduced by DiPerna and, based on the estimate
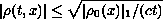
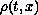 is shown to be a
is shown to be a
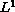 -entropy
solutions for the Cauchy problem
of the scalar conservation law with
-entropy
solutions for the Cauchy problem
of the scalar conservation law with