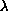 -lemma
-lemma
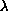 -lemma
-lemma
Victoria Rayskin
Abstract:
The well known
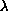 -lemma
[3] states the following:
Let
-lemma
[3] states the following:
Let
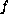 be a
be a
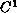 -diffeomorphism of
-diffeomorphism of
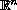 with a
hyperbolic fixed point at 0 and
with a
hyperbolic fixed point at 0 and
 - and
- and
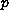 -dimensional stable
and unstable manifolds
-dimensional stable
and unstable manifolds
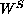 and
and
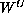 , respectively
(
, respectively
(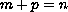 ).
Let
).
Let
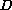 be a
be a
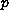 -disk
in
-disk
in
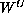 and
and
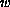 be another
p-disk
in
be another
p-disk
in
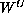 meeting
meeting
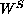 at some point
at some point
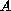 transversely. Then
transversely. Then
 contains
contains
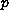 -disk arbitrarily
-disk arbitrarily
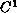 -close to
-close to
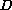 .
In this paper we will show that the same
assertion still holds outside of an arbitrarily small neighborhood
of 0,
even in the case of non-transverse homoclinic
intersections with finite order of contact, if we assume that 0
is a low order non-resonant point.
.
In this paper we will show that the same
assertion still holds outside of an arbitrarily small neighborhood
of 0,
even in the case of non-transverse homoclinic
intersections with finite order of contact, if we assume that 0
is a low order non-resonant point.
Submitted November 4, 2002. Published April 11, 2003.
Math Subject Classifications: 37B10, 37C05, 37C15, 37D10.
Key Words: Homoclinic tangency, invariant manifolds, lambda-Lemma,
order of contact, resonance
Show me the PDF file (227K), TEX file for this article.