Electron. J. Diff. Eqns.,
Vol. 2003(2003), No. 46, pp. 1-31.
On uniqueness and existence of entropy
solutions of weakly coupled systems
of nonlinear degenerate parabolic equations
Helge Holden, Kenneth H. Karlsen, & Nils H. Risebro
Abstract:
We prove existence and uniqueness of entropy solutions for
the Cauchy problem of weakly coupled systems of nonlinear
degenerate parabolic equations. We prove existence of an
entropy solution by demonstrating that the Engquist-Osher
finite difference scheme is convergent and that any limit
function satisfies the entropy condition. The convergence
proof is based on deriving a series of a priori estimates
and using a general
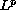 compactness criterion.
The uniqueness proof is an adaption of Kruzkov's
``doubling of variables'' proof. We also present a numerical
example motivated by biodegradation in porous media.
compactness criterion.
The uniqueness proof is an adaption of Kruzkov's
``doubling of variables'' proof. We also present a numerical
example motivated by biodegradation in porous media.
Submitted October 18, 2002. Published April 22, 2003.
Math Subject Classifications: 35K65, 65M12, 35L65.
Key Words: Nonlinear degenerate parabolic equations,
weakly coupled systems, entropy solution, uniqueness,
existence, finite difference method
Show me the
PDF file (749K),
TEX file for this article.
 |
Helge Holden
Department of Mathematical Sciences
Norwegian University of Science and Technology
NO--7491 Trondheim, Norway
email: holden@math.ntnu.no
http://www.math.ntnu.no/~holden |
|---|
 |
Kenneth H. Karlsen
Department of Mathematics
University of Bergen
Johs. Brunsgt. 12
N-5008 Bergen, Norway
e-mail: kennethk@mi.uib.no
http://www.mi.uib.no/~kennethk |
|---|
 |
Nils H. Risebro
Department of Mathematics
University of Oslo
P.O. Box 1053, Blindern
N-0316 Oslo, Norway
e-mail: nilshr@math.uio.no
http://www.math.uio.no/~nilshr |
|---|
Return to the EJDE web page
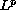 compactness criterion.
The uniqueness proof is an adaption of Kruzkov's
``doubling of variables'' proof. We also present a numerical
example motivated by biodegradation in porous media.
compactness criterion.
The uniqueness proof is an adaption of Kruzkov's
``doubling of variables'' proof. We also present a numerical
example motivated by biodegradation in porous media.


