Electron. J. Diff. Eqns., Vol. 2003(2003), No. 53, pp. 1-5.
Blow up of solutions to semilinear wave equations
Mohammed Guedda
Abstract:
This work shows the absence of global solutions to the
equation
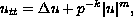
in the Minkowski space
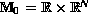 ,
where
,
where
 ,
,
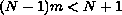 , and
, and
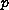 is a conformal factor
approaching 0 at infinity.
Using a modification of the method of conformal compactification,
we prove that any solution develops a singularity at a finite time.
is a conformal factor
approaching 0 at infinity.
Using a modification of the method of conformal compactification,
we prove that any solution develops a singularity at a finite time.
Submitted November 15, 2002. Published May 3, 2003.
Math Subject Classifications: 35L70, 35B40, 35L15.
Key Words: Blow up, conformal compactification.
Show me the
PDF file (180K),
TEX file for this article.
 |
Mohammed Guedda
Lamfa, CNRS UMR 6140
Universite de Picardie Jules Verne
Faculte de Mathematiques et d'Informatique
33, rue Saint-Leu 80039,
Amiens, France
email: guedda@u-picardie.fr
|
|---|
Return to the EJDE web page
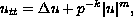
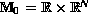 ,
where
,
where
 ,
,
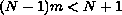 , and
, and
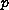 is a conformal factor
approaching 0 at infinity.
Using a modification of the method of conformal compactification,
we prove that any solution develops a singularity at a finite time.
is a conformal factor
approaching 0 at infinity.
Using a modification of the method of conformal compactification,
we prove that any solution develops a singularity at a finite time.
