Electron. J. Diff. Eqns.,
Vol. 2003(2003), No. 58, pp. 1-19.
Existence of positive solutions for some polyharmonic nonlinear
boundary-value problems
Habib Maagli, Faten Toumi, & Malek Zribi
Abstract:
We present existence results for the polyharmonic nonlinear
elliptic boundary-value problem
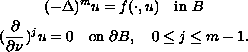
(in the sense of distributions), where
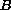 is the unit ball in
is the unit ball in
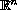 and
and
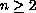 .
The nonlinearity
.
The nonlinearity
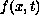 satisfies
appropriate conditions related to a Kato class of functions
satisfies
appropriate conditions related to a Kato class of functions
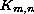 .
Our approach is based on estimates for the polyharmonic Green function
with zero Dirichlet boundary conditions and on the Schauder fixed point
theorem.
.
Our approach is based on estimates for the polyharmonic Green function
with zero Dirichlet boundary conditions and on the Schauder fixed point
theorem.
Submitted April 2, 2003. Published May 20, 2003.
Math Subject Classifications: 34B27, 35J40
Key Words: Green function, positive solution, Schauder fixed point theorem,
singular polyharmonic elliptic equation.
Show me the
PDF file (262K),
TEX file for this article.
 |
Habib Maagli
Departement de Mathematiques
Faculte des Sciences de Tunis
Campus universitaire, 1060 Tunis, Tunisia
email: habib.maagli@fst.rnu.tn
|
|---|
 |
Faten Toumi
Departement de Mathematiques
Faculte des Sciences de Tunis
Campus universitaire, 1060 Tunis, Tunisia
email: toumifaten@yahoo.fr |
|---|
 |
Malek Zribi
Departement de Mathematiques
Faculte des Sciences de Tunis
Campus universitaire, 1060 Tunis, Tunisia
email: malek.Zribi@insat.rnu.tn |
|---|
Return to the EJDE web page
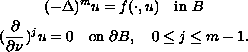
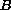 is the unit ball in
is the unit ball in
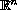 and
and
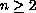 .
The nonlinearity
.
The nonlinearity
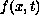 satisfies
appropriate conditions related to a Kato class of functions
satisfies
appropriate conditions related to a Kato class of functions
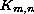 .
Our approach is based on estimates for the polyharmonic Green function
with zero Dirichlet boundary conditions and on the Schauder fixed point
theorem.
.
Our approach is based on estimates for the polyharmonic Green function
with zero Dirichlet boundary conditions and on the Schauder fixed point
theorem.


