We consider the Schrodinger type differential expression
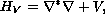
where
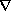 is a
is a
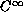 -bounded
Hermitian connection on a Hermitian vector bundle
-bounded
Hermitian connection on a Hermitian vector bundle
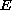 of bounded
geometry over a manifold of bounded geometry
of bounded
geometry over a manifold of bounded geometry
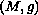 with metric
with metric
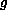 and positive
and positive
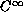 -bounded
measure
-bounded
measure
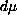 , and
, and
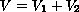 , where
, where
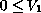 in
in
 and
and
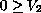 in
in
 are linear
self-adjoint bundle endomorphisms. We give a sufficient condition
for self-adjointness of the operator
are linear
self-adjoint bundle endomorphisms. We give a sufficient condition
for self-adjointness of the operator
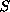 in
in
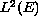 defined by
defined by
 for all
for all
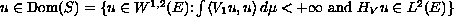 .
The proof follows the scheme of Kato, but
it requires the use of more general version of Kato's inequality
for Bochner Laplacian operator as well as a result on the
positivity of
.
The proof follows the scheme of Kato, but
it requires the use of more general version of Kato's inequality
for Bochner Laplacian operator as well as a result on the
positivity of
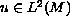 satisfying the equation
satisfying the equation
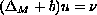 ,
where
,
where
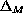 is the scalar Laplacian on
is the scalar Laplacian on
 ,
,
 is a constant and
is a constant and
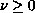 is a positive
distribution on
is a positive
distribution on
 .
.
