Electron. J. Diff. Eqns., Vol. 2003(2003), No. 68, pp. 1-12.
Global solution for the Kadomtsev-Petviashvili equation (KPII)
in anisotropic Sobolev spaces of negative indices
Pedro Isaza J. & Jorge Mejia L.
Abstract:
It is proved that the Cauchy problem for the Kadomtsev-Petviashvili
equation (KPII) is globally well-posed for initial data in anisotropic
Sobolev spaces
 with
with
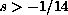 .
The extension of a local solution to a solution in an arbitrary interval
is carried out by means of an almost conservation property of the
.
The extension of a local solution to a solution in an arbitrary interval
is carried out by means of an almost conservation property of the
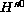 norm of the solution.
norm of the solution.
Submitted September 13, 2002. Published June 13, 2003.
Math Subject Classifications: 35Q53, 37K05.
Key Words: Nonlinear dispersive equations, global solutions,
almost conservation laws.
Show me the
PDF file (241K),
TEX file for this article.
 |
Pedro Isaza J.
Escuela de Matematicas
Universidad Nacional de Colombia
A. A. 3840 Medellin, Colombia
email: pisaza@perseus.unalmed.edu.co
|
|---|
 |
Jorge Mejia L.
Escuela de Matematicas
Universidad Nacional de Colombia
A. A. 3840 Medellin, Colombia
email: jemejia@perseus.unalmed.edu.co |
|---|
Return to the EJDE web page
 with
with
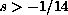 .
The extension of a local solution to a solution in an arbitrary interval
is carried out by means of an almost conservation property of the
.
The extension of a local solution to a solution in an arbitrary interval
is carried out by means of an almost conservation property of the
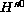 norm of the solution.
norm of the solution.

