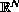
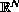
Joao Marcos do O & Everaldo S. Medeiros
Abstract:
In this work we establish some properties of the solutions
to the quasilinear second-order problem
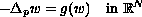
where
 is the
is the
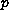 -Laplacian
operator and
-Laplacian
operator and
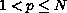 .
We study a
mountain pass characterization of least energy solutions of this
problem. Without assuming the monotonicity of the function
.
We study a
mountain pass characterization of least energy solutions of this
problem. Without assuming the monotonicity of the function
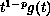 ,
we show that the Mountain-Pass value gives the
least energy level. We also prove the exponential decay of the
derivatives of the solutions.
,
we show that the Mountain-Pass value gives the
least energy level. We also prove the exponential decay of the
derivatives of the solutions.
Submitted June 3, 2003. Published August 11, 2003.
Math Subject Classifications: 35J20, 35J60.
Key Words: Variational methods, minimax methods,
superlinear elliptic problems, p-Laplacian,
ground-states, moutain-pass solutions
Show me the PDF file (253K), TEX file for this article.
 |
Joao Marcos do O Departamento de Matematica, Univ. Fed. Paraiba 58059-900 Joao Pessoa, PB, Brazil email: jmbo@mat.ufpb.br |
|---|---|
 |
Everaldo S. Medeiros Departamento de Matematica, Univ. Fed. Paraiba 58059-900 Joao Pessoa, PB, Brazil email: everaldo@mat.ufpb.br |
Return to the EJDE web page