Electron. J. Diff. Eqns., Vol. 2004(2004), No. 101, pp. 1-13.
The critical case for a semilinear weakly hyperbolic equation
Luca Fanelli, Sandra Lucente
Abstract:
We prove a global existence result for the Cauchy problem, in the
three-dimensional space, associated with the equation
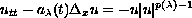
where
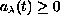 and behaves as
and behaves as
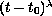 close to some
close to some
 with
with
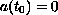 ,
and
,
and
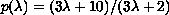 with
with
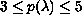 .
This means that we deal with the superconformal, critical
nonlinear case. Moreover we assume a small initial energy.
.
This means that we deal with the superconformal, critical
nonlinear case. Moreover we assume a small initial energy.
Submitted July 22, 2004. Published August 24, 2004.
Math Subject Classifications: 35L70, 35L15, 35L80.
Key Words: Global existence; semilinear wave equations.
Show me the
PDF file (265K),
TEX file for this article.
 |
Luca Fanelli
Dipartimento di Matematica
Universita "La Sapienza" di Roma
Piazzale Aldo Moro 2, I-00185 Roma, Italy
email: fanelli@mat.uniroma1.it |
|---|
 |
Sandra Lucente
Dipartimento di Matematica
Universita degli Studi di Bari
Via E. Orabona 4, I-70125 Bari, Italy
email: lucente@dm.uniba.it |
|---|
Return to the EJDE web page
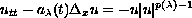
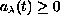 and behaves as
and behaves as
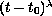 close to some
close to some
 with
with
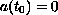 ,
and
,
and
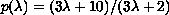 with
with
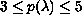 .
This means that we deal with the superconformal, critical
nonlinear case. Moreover we assume a small initial energy.
.
This means that we deal with the superconformal, critical
nonlinear case. Moreover we assume a small initial energy.

