Electron. J. Diff. Eqns., Vol. 2004(2004), No. 106, pp. 1-9.
Pyramidal central configurations and perverse solutions
Tiancheng Ouyang, Zhifu Xie, Shiqing Zhang
Abstract:
For
 -body problems, a central configuration (CC) plays an
important role. In this paper, we establish the relation between
the spatial pyramidal central configuration (PCC) and the
planar central configuration. We prove that the base of PCC is
also a CC and we also prove that for some given conditions a
planar CC can be extended to a PCC. In particular, if the
pyramidal central configuration has a regular polygon base, then
the masses of base are equal and the distance between the top
vertex and the base is fixed and the mass of the top vertex is
selective. Furthermore, the pyramidal central configuration gives
rise to an example of a perverse solution in
-body problems, a central configuration (CC) plays an
important role. In this paper, we establish the relation between
the spatial pyramidal central configuration (PCC) and the
planar central configuration. We prove that the base of PCC is
also a CC and we also prove that for some given conditions a
planar CC can be extended to a PCC. In particular, if the
pyramidal central configuration has a regular polygon base, then
the masses of base are equal and the distance between the top
vertex and the base is fixed and the mass of the top vertex is
selective. Furthermore, the pyramidal central configuration gives
rise to an example of a perverse solution in
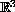 .
.
Submitted December 6, 2003. Published September 10, 2004.
Math Subject Classifications: 37N05, 70F10, 70F15.
Key Words: n-body problems; pyramidal central configuration;
regular polygonal base; perverse solutions.
Show me the
PDF file (205K),
TEX file for this article.
| |
Tiancheng Ouyang
Department of Mathematics, Brigham Young University
Provo, Utah 84604, USA
email: ouyang@math.byu.edu |
|---|
 |
Zhifu Xie
Department of Mathematics, Brigham Young University
Provo, Utah 84604, USA
email: zhifu@math.byu.edu |
|---|
| |
Shiqing Zhang
Department of Mathematics
Yangzhou University, Yangzhou, China
email: shiqing2001@163.net |
|---|
Return to the EJDE web page
 -body problems, a central configuration (CC) plays an
important role. In this paper, we establish the relation between
the spatial pyramidal central configuration (PCC) and the
planar central configuration. We prove that the base of PCC is
also a CC and we also prove that for some given conditions a
planar CC can be extended to a PCC. In particular, if the
pyramidal central configuration has a regular polygon base, then
the masses of base are equal and the distance between the top
vertex and the base is fixed and the mass of the top vertex is
selective. Furthermore, the pyramidal central configuration gives
rise to an example of a perverse solution in
-body problems, a central configuration (CC) plays an
important role. In this paper, we establish the relation between
the spatial pyramidal central configuration (PCC) and the
planar central configuration. We prove that the base of PCC is
also a CC and we also prove that for some given conditions a
planar CC can be extended to a PCC. In particular, if the
pyramidal central configuration has a regular polygon base, then
the masses of base are equal and the distance between the top
vertex and the base is fixed and the mass of the top vertex is
selective. Furthermore, the pyramidal central configuration gives
rise to an example of a perverse solution in
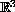 .
.
