Consider the Dirichlet eigenvalue problem associated with the real two-term weighted Sturm-Liouville equation
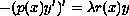
on the finite interval [a,b]. This eigenvalue problem will be called degenerate provided its spectrum fills the whole complex plane. Generally, in degenerate cases the coefficients
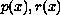must each be sign indefinite
on [a,b]. Indeed, except in some special cases, the quadratic
forms induced by them on appropriate spaces must also be indefinite.
In this note we present a necessary and sufficient condition
for this boundary problem to be degenerate. Some extensions are noted.
